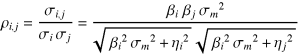Stress Markets and Correlation

We have all heard statements to the effect that “During market corrections all correlations tend to one.”  Often it’s accompanied either by an explanation unsupported by any real critical thinking or presented as some deep impenetrable mystery of finance. The objective of this post is to illustrate a single and simple concept that is more than adequate to explain this phenomenon. The approach used is that of a Gedandanken-Experiment, which is not actually an experiment but the application of a model stripped down to its essential elements to explore a situation or idea. What follows assumes that the reader has a basic knowledge of probability and statistics and high school level algebra skills.

The Capital Asset Pricing Model

We will use the equity market and the Capital Pricing Asset Model (CAPM) as the basis for our Gedanken-Experiment. Despite its limitations and the fact few practitioners believe that it is anything approaching a complete description of a stock’s behavior, it will be enough in that is captures some reasonable amount of reality: Individual stocks clearly move in concert with the market  and some stocks do so more or less than do others. The CAPM asserts that at time t the return r of stock i is expressed in terms of the risk-free rate r_f , its exposure the market (or beta) β_i, the market return m, and a zero-mean noise term ε that is uncorrelated to the market:

Let σ_m² be the variance of the market return and η_i² the variance of the noise term, then the variance of the stock σ_i² is:

The market variance is also called the systematic variance and the noise variance is also called the unsystematic or idiosyncratic variance.

The noise terms of different stocks are uncorrelated; hence, the sole source of covariance σ_i,j between stocks i and j comes from their respective betas. The definition of covariance and some simple alegbra suffices to show:

The correlation (in the sense here it is usually called r-squared)  ρ_i,j  is then by definition:

Heteroskedasticity

When we look at markets, variances are not constant but wax and wane over time. The property of having such time-varying variance is termed heteroskedasticity. In practice, both the systematic and unsystematic variances are heteroskedastic. However, if we view the variance as a measure of new information, then during periods of market stress, it is obviously the market or systematic variance  that will dominate.

The Experiment

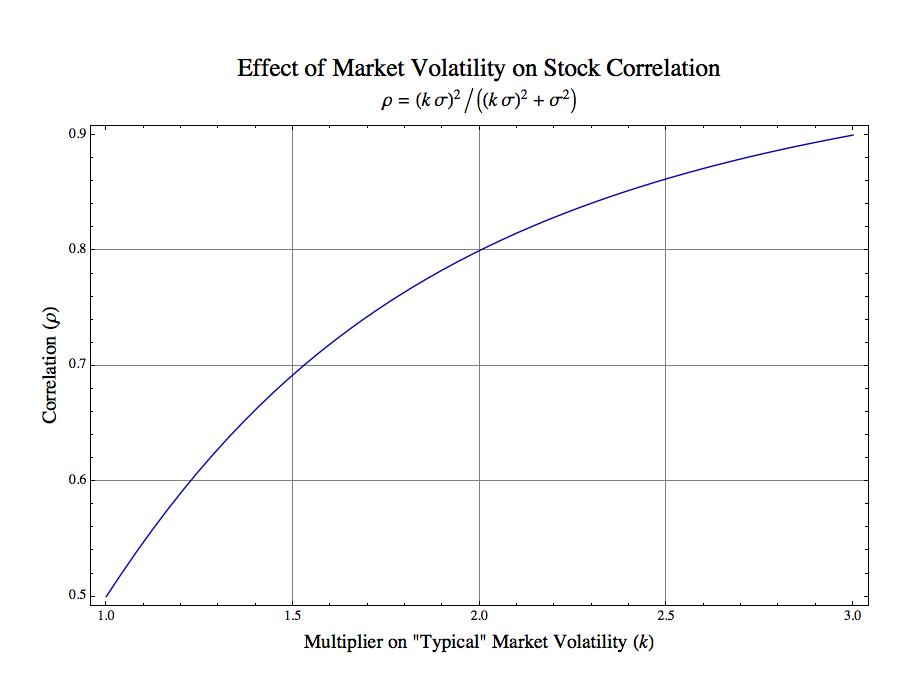
Let us consider a simple case in which we have two stocks which during “typical” market environments have equal unsystematic variances which are in turn equal to the market variance. Call that common value σ². To further simplify the exposition we will assume both stocks have betas of one. Finally, we will characterize a stress parameter k which is a multiplier on the typical market volatility (the square root of variance, the standard deviation), i.e., kσ. We substitute these values into the above expression and simplify to yield the correlation ρ of our stress model:

During normal markets k = 1 and the correlation is 0.5. To examine what happens during stress periods we plot the correlation ρ as a function of market stress k:

 As the graph above shows when the market volatility increases by a factor of 2, the correlation increases from 0.5 to 0.8. When it increases to 3, the correlation is 0.9. If one wanted to estimate a value for our stress parameter k during serious market corrections, then a value of 3 is probably conservative. Clearly, the increase in market volatility, independent of other effects, is sufficient to explain the dramatic increase in correlation across the market.

 Other Effects

Are there other effects that we have not considered here? Almost certainly. For example, there is some evidence for “stress” betas. In other words, not only is there an increase in market volatility but the betas which link stocks to the market also appear to increase during stress periods.

As we mentioned, there may be some concomitant increase in non-systematic volatility. However, if one thinks it through, then any effect shared across stocks generally is a systematic effect, not an idiosyncratic one. It is likely that it is the increase in systematic volatility that dominates.

Conclusion

In our simple model conservative increases in market volatility during stress periods cause dramatic increases in market correlation. When markets correct, then systematic  information is absorbed in common across investments, and market heteroskedasticity is sufficient to explain the observed increase in general correlation.