Stress Markets and Correlation
We have all heard statements to the effect that “During market corrections all correlations tend to one.” Often it’s accompanied either by an explanation unsupported by any real critical thinking or presented as some deep impenetrable mystery of finance. The objective of this post is to illustrate a single and simple concept that is more than adequate to explain this phenomenon. The approach used is that of a Gedandanken-Experiment, which is not actually an experiment but the application of a model stripped down to its essential elements to explore a situation or idea. What follows assumes that the reader has a basic knowledge of probability and statistics and high school level algebra skills.
The Capital Asset Pricing Model
We will use the equity market and the Capital Pricing Asset Model (CAPM) as the basis for our Gedanken-Experiment. Despite its limitations and the fact few practitioners believe that it is anything approaching a complete description of a stock’s behavior, it will be enough in that is captures some reasonable amount of reality: Individual stocks clearly move in concert with the market and some stocks do so more or less than do others. The CAPM asserts that at time t the return r of stock i is expressed in terms of the risk-free rate rf , its exposure the market (or beta) βi, the market return m, and a zero-mean noise term ε that is uncorrelated to the market:
Let σm2 be the variance of the market return and ηi2 the variance of the noise term, then the variance of the stock σi2 is:
The market variance is also called the systematic variance and the noise variance is also called the unsystematic or idiosyncratic variance.
The noise terms of different stocks are uncorrelated; hence, the sole source of covariance σi,j between stocks i and j comes from their respective betas. The definition of covariance and some simple alegbra suffices to show:
The correlation (in the sense here it is usually called r-squared) ρi,j is then by definition:
Heteroskedasticity
When we look at markets, variances are not constant but wax and wane over time. The property of having such time-varying variance is termed heteroskedasticity. In practice, both the systematic and unsystematic variances are heteroskedastic. However, if we view the variance as a measure of new information, then during periods of market stress, it is obviously the market or systematic variance that will dominate.
The Experiment
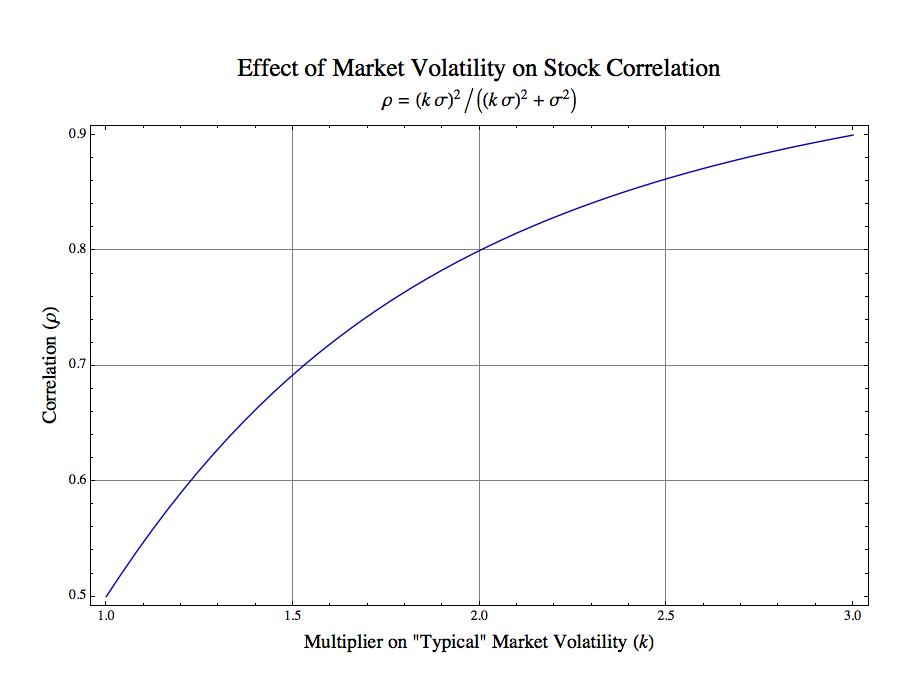
Let us consider a simple case in which we have two stocks which during “typical” market environments have equal unsystematic variances which are in turn equal to the market variance. Call that common value σ2. To further simplify the exposition we will assume both stocks have betas of one. Finally, we will characterize a stress parameter k which is a multiplier on the typical market volatility (the square root of variance, the standard deviation), i.e., kσ. We substitute these values into the above expression and simplify to yield the correlation ρ of our stress model:
During normal markets k = 1 and the correlation is 0.5. To examine what happens during stress periods we plot the correlation ρ as a function of market stress k:
As the graph above shows when the market volatility increases by a factor of 2, the correlation increases from 0.5 to 0.8. When it increases to 3, the correlation is 0.9. If one wanted to estimate a value for our stress parameter k during serious market corrections, then a value of 3 is probably conservative. Clearly, the increase in market volatility, independent of other effects, is sufficient to explain the dramatic increase in correlation across the market.
Other Effects
Are there other effects that we have not considered here? Almost certainly. For example, there is some evidence for “stress” betas. In other words, not only is there an increase in market volatility but the betas which link stocks to the market also appear to increase during stress periods.
As we mentioned, there may be some concomitant increase in non-systematic volatility. However, if one thinks it through, then any effect shared across stocks generally is a systematic effect, not an idiosyncratic one. It is likely that it is the increase in systematic volatility that dominates.
Conclusion
In our simple model conservative increases in market volatility during stress periods cause dramatic increases in market correlation. When markets correct, then systematic information is absorbed in common across investments, and market heteroskedasticity is sufficient to explain the observed increase in general correlation.

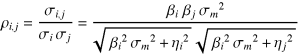
Thank you Robert, for this clear and interesting explanation. As a mathematician, i appreciate the simplicity of your explanation.
I have a similar view, although I don’t base it in CAPM. Covariance of stocks is consistent with factor models (whether for CAPM, APT, or whatever reason) and some of the factors have bursty returns, and some of the factors (one, I think) correspond to leverage. So if things get “scary” for whatever reason, the leverage factor gets excited (because many market participants deleverage – voluntarily or not). So what would the factor loads be in a “leverage” factor? They would look like the leverage available in that instrument. And in the US equities market, just about anyone can buy many stocks at 15% margin – irrespective of which stock, (exceptions being pink sheeted stocks, etc.).So the factor loads for leverage will be expected to be pretty uniform, which is why the asset covariance in events where leverage is highly excited is dominated by that factor, which has all assets positively correlated.
The factor return for the leverage factor will normally be small with a positive bias, and occasionally very large negative values, reflecting the widely held view that equities markets crash “down” but rarely crash “up”.
The picture is not completely at odds with your explanation – if you estimate ‘uniform’ betas for stocks over a long period of time, then you will end up with a covariance model that is a blend of the event covariances and the typical covariances, and leverage factor loads will end up biasing the “market” factor loads.
In keeping with the concept of a Gedanken-Experiment, I used the CAPM, a single factor model, as the minimum level of complexity to illustrate how heteroskedasticity affects correlation. Certainly a multi-factor model such as the Arbitrage Pricing Theory (APT) provides a more representative model, but the effect of systematic heteroskedasticity is the same.
The deleverage effect you mention is real, but I believe that it is more of an explanation why stress markets have negative returns and high volatility; i.e., it is the cause of the cause. It also probably contributes to the increase in general correlation in other ways, but the data show that most of the stress correlation effect can be accounted for by the increase in systematic volatility.
Are you sure that the correlation function is right? I only get an answer that matches the graph if I scale by k-squared.
The scaling k is on the volatility (i.e., standard deviation or square root of the variance). The idea that market moves can be k = 3 times bigger during a correction than during a non-stress period is something people can more easily judge the reasonableness of. Thus, rho = sigma^2 / ((k * sigma)^2 + sigma^2) as shown in the last equation and on the subtitle of the plot. I’m sorry if this was confusing and will try to be less so in subsequent posts. As a mathematician I tend to think in terms of the covariance and correlation matrices rather than in terms that many texts use to describe univariate OLS. The value at k = 3 is an r-squared of 0.9, which some would call a “correlation” of 0.95.
There is a typo in the equations. You have to multiply the variance in the numerator by k, since it’s the market variance. Only than do you get an increasing correlation for the stocks.
Sorry, I meant the standard deviation in the numerator, so the variance times k^2
Thank you for reading the post carefully. You are, of course, correct, and I’ve fixed the typo in the equation in both the text and plot.
I’m just curious, doesn’t wordpress have a LaTeX plugin (something like ?)…
?)…
(I hasten to add, for display style equations, etc.)
for display style equations, etc.)
Yes, it does, but I found it to be kind of kludgy–at least for the tools I usually use. My stuff doesn’t seem to come out as nicely formatted as the integral in your comment. Could you send me the plaintext that you used to create it. Thanks.
Oh, my, the trick is quite simple. You simply write the
Slatex ...Sas usual (I use capital “S” instead of dollar signs, just for demonstrations). The first thing you do:Slatex \displaystyle{ ... }SWrapping everything inside a
\displaystyle{...}macro makes it quite pretty, like the latter integral. This is what happens inside equation environments in LaTeX.Neglecting it makes the LaTeX math be inline, like what happens in
\(...\).[My goodness, I hope that all renders correctly!]
I was leaving out the \displaystyle{ … }. This simple fix will make my life a lot easier. I’m new to Word Press, and this sort of “training” is much appreciated!
Following your great thoughts on Twitter, and come here following your link.
You may wish to check a couple of typos I have spotted reading the article:
1. There is an “i” in the denominator of the formula [ following the sentence: “The correlation (in the sense here it is usually called r-squared)” ] which is probably mean to be a “j” (I think)
2. “alegbra” in “some simple alegbra”
3. The “r-squared” is probably meant to be be simply “r” (as it is not squared now, maybe it was in a previous version of the article ).
Also, your final formula is, actually, simply: r = k^2 / ( k^2 + 1 ) also equal to
1 – 1 / ( k^2 + 1), where clearly the second term quickly vanishes as k diverges.
If you like, I will later read also more carefully the content and, in case, provide some feedback on the conceptual part. Ah, btw, in case, for formulas, it may very simple and convenient to use mathjax: http://www.mathjax.org/ (if your CMS allows it, of course).
Thanks, for your kind words on my Twitter posts (as @financequant) and your feedback on the typos. Regarding the r-squared, the reference is correct. What I had called the correlation (the covariance divided by the product of the standard deviations) is what most stat software would call r-squared. Finally, I did come across the fact that I could use LaTeX embedded in my posts and will do so in future ones.
>Thanks, for your kind words on my Twitter posts (as @financequant) and your feedback
It’s a great honor for me to have the possibility to follow you, and learn from your great experience
> “(the covariance divided by the product of the standard deviations) is what most stat software would call r-squared”
I am sure that some financial software might possibly use the terminology in that way, but, imho, it would be misleading. But let me explain better my view, and please do advise if I am wrong.
“covariance divided by the product of the standard deviations” is what we normally call “r”, while “r-squared” is, as the name suggests, is the square of that (in the specific case of linear model), or, more in general, it is a quadratic measure of fit (coefficient of determination).
There is also an evident reason why something called “r-squared” cannot be possibly defined just as a “normalized covariance” (which is r). In fact, a covariance is “signed” (can take *any* negative value) while “r-squared”, being “squared”, can only be nonnegative (0-1, or 0-100 if %).
Thus,”r-squared” (in the linear model case) has the square of the covariance at the numerator, and it cannot be defined, imho, as “covariance divided by the product of the standard deviations”.
See also, for instance, this reference (where the square of covariance at numerator is clearly shown):
http://stats.stackexchange.com/questions/17050/explanation-for-r-squared-as-ratio-of-covariances-and-variances
So the 4-th formula from top would need some adjustments, imho.
The more conceptual point is that “r squared” is, in general, a measure of goodness of fit (coefficient of determination) or proportion of response variation “explained” by the regressors in a model, and, in the linear case it just “happens” to be algebraically equal to the square of the coefficient of correlation r (this is apparently the reason of the name): R^2 =r^2 =[cor(x,y)]^2
cfr: http://en.wikipedia.org/wiki/Coefficient_of_determination
> “equal unsystematic variances which are in turn equal to the market variance.
Call that common value σ^2. To further simplify the exposition we will assume both stocks have betas of one.”
Let me propose an interpretation, and, please, advise if I am missing the point.
Assuming the betas = 1, you are constraining both stocks to “same direction as, and about the same amount as the movement of the benchmark”
http://en.wikipedia.org/wiki/Beta_(finance)
This would cause, by transitivity, the correlation of the 2 stocks to be equal to +1.
What k^2 / ( k^2 + 1 ) -> +1 seems to be telling, in intuitive terms, is that, by “neglecting” (in relative terms) what is here called the “idiosyncratic variance” (k large), we end up letting emerge the correlation = +1, which in fact was assumed in the first place, by setting equal systematic variances and betas = 1.
It seems to me the conceptual thesis here is essentially assumed, and not actually derived or justified through “the experiment”.
On a more practical perspective, take, for instance, two instruments like “fas” and “faz”. It does not matter what volatility they or “spy” exhibit, and whatever else stress condition in the mkt, “faz” will always have a -1 < r < 0 with both "fas" and "spy", no matter what, and such correlation will not converge anywhere, but rather randomly fluctuate in the negative interval. This is simply by construction.
However, even finding a more convincing mathematical argument involving |r| and a local approximation (which is actually conceivable, imho), a broader objection could be that r captures, in any case, only the "linear component" of a relationship, while linearity is an elementary abstraction created by mathematicians, and, imho, mkt could not care less about it, unless we consider local approximations. And, in fact, the geometry of reality seems much more of random and fractal nature, at least in its initial or simplest and primitive expressions.
To make another practical example assume you have two stocks like for instance "spy" and "vxx". Imagine a short period with violent moves. Say "spy" goes up and then turns down (or vice versa). In the entire period, you would see an r closer to 0. Looking at half period, you would see an r closer to -1.
(To transcend linearity limitations there are dependence metrics which may suit better the analysis)
As a mathematician I think in terms of the components of the correlation matrix. The term “r-squared” is not one that I use myself. I’ll double check on the terminology and edit the post if necessary; it may be easiest to simply take out the reference as it is unnecessary to the argument being presented, In any event, I appreciate your careful reading.
Yes, the correlation makes most sense when talking about a linear relationship. I used the CAPM, which is linear, simply as an approximation of reality. There are economic arguments that this linear behavior dominates. Increasing the volatility of a factor that is common to two instruments will increase the tendency of those instruments to move together–whether positively or negatively.
The reason I left the in the expression for
in the expression for 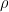 is to make the source of the relationship clearer. One could, of course, factor it out.
is to make the source of the relationship clearer. One could, of course, factor it out.
The fourth equation is correct. The covariance between two instruments in the CAPM is the product of their respective times the market variance. An instrument’s variance is its
times the market variance. An instrument’s variance is its  square times the market variance plus the error variance. The expression follows.
square times the market variance plus the error variance. The expression follows.
The fact that two stocks have the same doesn’t mean that their correlation is necessarily high. The effects of the error variances have to be accounted for.
doesn’t mean that their correlation is necessarily high. The effects of the error variances have to be accounted for.
Pingback: maillot de foot